안녕하세요, Lead Researcher 박진우 입니다.
지난 1편에서는 기존 Pruning 방법들을 미리 레이어마다 자를 비율을 정해 놓는 predefined과 자동으로 학습과정에서 찾게 하는 automatic으로 나누고, automatic에서도 filter/channel 단위로 잘라내는 structured pruning과 weight element 단위로 잘라내는 unstructured pruning으로 구분할 수 있었습니다. 물론 predefined은 structured pruning으로 취급되었습니다.
이때, 저자들이 주장하는 내용은 structured pruning을 진행할 때, pruning을 진행한 후 남은 weight 값을 그대로 가져와 fine-tuning 하는 것보다, 남은 구조만 가져오고 새로 weight initialization을 진행한 후 처음부터 새로 학습(train from scratch)하는 방법이 더 높은 정확도를 보인다는 사실을 보여주면서 '기존 pruning 방법들로 배우는 것은 중요한 weight들을 찾아내는 것보다 중요한 구조를 찾아내는 것에 가깝다'라는 주장을 보입니다. 이 주장들을 뒷받침하기 위해, 저자들은 기존에 있던 여러 가지 pruning 방법들에 대해 실험을 진행하였습니다.
이번 2편에서 살펴보고자 하는 부분들은 이 실험들을 소개하는 동시에, 각각의 기존 pruning 방법들에 대해 알아보는 시간을 가지고자 합니다.

Experiments
Predefined Structured Pruning
<L1-norm based Filter Pruning (Li et al., 2017)>은 filter/channel pruning의 가장 초기 논문 중 하나입니다. 해당 논문에서 말하고 있는 filter pruning은 매우 간단한 방법으로, 학습시킨 후 각 필터마다 L1 norm, 즉 필터에 속한 가중치 값들의 절댓값의 합을 구해 결과값이 작은 순서대로 pruning하는 방법입니다. 즉 절댓값이 큰 필터일수록 중요하다고 가정하는 것입니다. 원문을 그대로 소개해 드리자면 아래와 같습니다.

L1-norm 논문에서 해당 방안으로 pruning을 진행한 결과는 아래와 같습니다.

표를 보시면 아시겠지만, VGG-16의 경우 64% 정도의 가중치를 제거할 수 있었지만, ResNet의 경우 13.7%, 32.4%, 10.8% 등으로 제거한 가중치의 양이 그리 많다고 볼 수는 없다는 점입니다. 여기서 저희는 Filter의 L1-norm이 해당 Filter의 중요도를 나타내기에는 부족하다는 사실을 유추할 수 있습니다.
추가적으로, 표 위의 설명에 보시면 “Training a pruned model from scratch performs worse than retraining a pruned model”이라는 설명이 붙어있는데, 이는 사실 ‘Rethinking’ 논문에서 주장하고 있는 내용과 위배되는 내용입니다. 어찌 된 일일까요? 일단 Rethinking 논문의 결과를 살펴봅시다.

Rethinking 논문의 결과로는 Scratch-E는 fine-tune과 거의 비슷한 정확도를 보여주며, Scratch-B는 확실하게 Scratch-E와 fine-tune보다 높은 정확도를 보여줍니다. 위의 표에서 볼 수 있는 결과는 크게 두 가지입니다. 첫 번째로, 일단 rethinking 논문에서 주장하는, predefined structured pruning의 경우 scratch부터 학습하는 것이 fine-tuning보다 좋다는 것을 이 결과는 뒷받침하고 있습니다. L1-norm pruning 논문에서는 더 좋지 않다고 되어있었지만, 개인적인 판단으로는 일단 정확도가 범위가 아닌 단일 정확도로 나와있었던 점으로 미루어보아 충분한 시도, 혹은 epoch 동안 학습시키는 실험이 이루어지지 못했거나, 혹은 앞서 Rethinking 논문에서 제안되었던 Scratch-B, 즉 computational budget을 생각하여 좀 더 오랜 epoch 동안 학습시키는 방법이 생각보다 더 효과적이었다고 생각됩니다.
<ThiNet (Luo et al., 2017)>은 weight 값 자체의 무언가가 아니라, 다음 layer의 activation 값에 가장 작은 영향을 주는 channel들을 greedy하게 자르는 방법입니다. 여기서 짚고 넘어가야 할 점은, weight filter의 channel을 자르는 것은 결국 input tensor의 특정 channel을 자르는 것이므로, 그 이전 layer의 filter를 자르는 것과 동치라는 것입니다. 이는 아래 그림을 보면 잘 나타나 있습니다.

ThiNet에서 풀고자 하는 최적화 문제는 아래와 같습니다. 특정 layer를 두고, 해당 layer의 필터 채널 일부가 잘린 후 나오는 output이 x_hat이라고 할 때, 원래의 output y와의 차이가 최소화되는 채널을 없애도록 하는 것입니다.

위의 최적화 문제를 잘 살펴보면, 결국 prune 후의 필터 채널들의 output이 원래와 차이가 적으려면 잘린 채널들에 의해 생성되는 input element 들의 전체 합이 가장 작은 것을 찾는 것과 같습니다. 즉 아래의 최적화 문제와 같습니다.
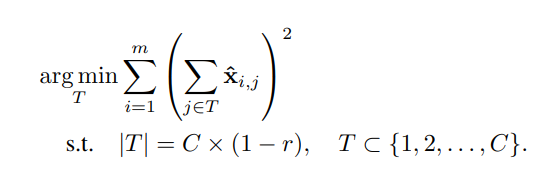
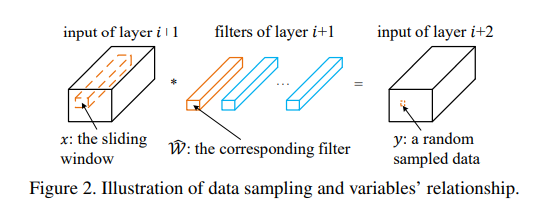
여기서 x와 y는 training imageset과 그 label이 아닌, 아래와 같이 특정 layer 사이에서의 input tensor와 output tensor element 간의 관계입니다. 여기서 i가 아니라 i+1이 되어 있는 이유는, 해당 과정은 i+1번째 필터의 채널들을 pruning하는 것이고, 결론적으로 i번째 필터를 자르는 것과 동치가 되기 때문입니다.
최종적으로 ThiNet의 pseudo code는 아래와 같습니다. (Eq. 6은 변형된 최적화 식입니다)

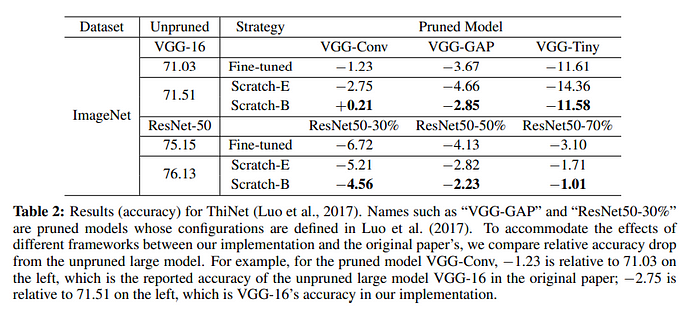
아래는 ThiNet을 이용하여 Rethinking 실험 프로세스를 진행한 결과입니다. ThiNet의 결과도 L1-norm과 마찬가지로, 대부분의 경우에서 Scratch-B가 제일 우세하며, ResNet의 경우 Scratch-E도 fine-tuning보다는 더 좋은 결과를 보여주고 있습니다. 다만 VGG의 경우, 특히 VGG-Tiny의 경우는 Scratch-E가 fine-tune보다 좋지 않은 모습을 보여줍니다. 논문에서는 해당 결과에 대해, VGG-Tiny의 경우 굉장히 많은 파라미터가 잘려나가기 때문에 Scratch-E만 진행할 경우 training budget 면에서 굉장히 많은 손해를 본다고 설명합니다.
<Regression based Feature Reconstruction (He et al., 2017b)>은 특정 레이어를 기준으로 그다음 레이어의 feature map reconstruction error을 최소화하는 방향으로 레이어의 channel을 제거하는 방안을 제시하고 있습니다. 바로 위에서 설명드렸던 ThiNet과 굉장히 비슷한 원리로 생각할 수 있는데, 다른 점이라면 이 논문에서는 ThiNet과 달리 LASSO regression, 즉 가중치의 L1-norm을 고려하는 방식으로 해결책을 제시한다는 점입니다.

위는 해당 논문에서 풀고자 하는 optimization problem입니다. 보시면 아시겠지만, 단순히 cross entropy loss term에 L1-norm을 추가하는 방식 등을 사용하는 것이 아닌, 위와 같은 최적화 문제를 (1) 일단 가중치 W를 고정시키고 channel selection 시 사용되는 scalar mask β를 구한 후, (2) 다시 β를 고정시킨 후 reconstruction error을 최소화하는 W를 구하는 단계를 반복적으로 진행하여 pruning을 진행한다고 합니다. 더욱 자세한 내용을 알고 싶으시다면 해당 논문을 참고 부탁드립니다.

LASSO regression을 사용한 channel pruning 논문 또한 scratch-B가 제일 우수한 모습을 보여주었습니다.
Automatic Structured Pruning
<Network Slimming (Liu et al., 2017)>은 각각의 channel에 주어지는 batch norm scaling factor에 대해 L1 norm loss term을 classification loss에 추가한 후, 이 scaling factor를 기준으로 작은 channel일수록 낮은 중요도로 보는 꽤나 직관적인 방법입니다.
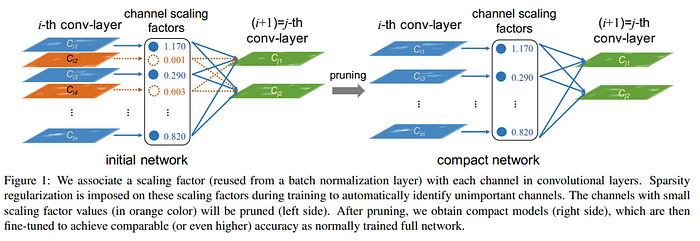

여기서 이 network slimming이 automatic structured pruning인 이유는, 해당 scaling factor들이 각각의 레이어뿐만이 아니라 모든 레이어에 걸쳐서 비교되기 때문에, 어떤 레이어에서 얼마만큼의 channel들이 잘려나갈지는 해당 과정이 이루어지기 전까지는 모른다는 점입니다.

Network slimming에 Fine-tune, scratch-E, scratch-B를 적용한 결과는 위와 같이 scratch-B가 대부분 가장 앞서고, scratch-E는 fine-tune보다 살짝 떨어지거나 혹은 비슷한 모습을 보이고 있습니다.
<Sparse Structure Selection (Huang & Wang, 2018)>은 Network Slimming에서 사용하던 방법처럼 특정 structure에 대해 부과된 scaling factor을 바탕으로 pruning 여부를 결정하는 방법입니다. 아래의 그림은 Sparse Structure Selection에서 하는 방법입니다.

위의 그림에서처럼, 해당 논문에서는 Block(가장 오른쪽), Group(가운데 부분), 그리고 Neuron(가장 오른쪽)에 scaling factor λ를 부여한 후 해당 λ를 Accelerated Proximal Gradient 방법으로 학습시키는 과정을 보여주고 있습니다.

아래는 이 Sparse Structure Selection에 Rethinking 방법론을 적용한 결과로, 마찬가지로 scratch-B가 가장 좋은 정확도를 보이는 것을 볼 수 있습니다.

위의 network slimming과 sparse structure selection을 통해, automatic pruning이라고 하더라도, structured pruning의 경우는 scratch-B가 가장 올바른 학습 방법이라고 생각될 수 있습니다.
Unstructured Magnitude-based pruning (Han et al., 2015)
<Unstructured magnitude-based weight pruning (Han et al., 2015)>는 앞서 1편에서 설명드렸듯 최근의 pruning 논문들 중 가장 초기작이라고 할 수 있으며, 기존의 딥러닝 모델들이 굉장히 over-parameterize 되어 있기 때문에 단순히 weight의 magnitude (절댓값) 기준으로 작은 것들을 잘라낸 후 fine-tuning 하는 것만으로도 많은 양의 가중치들을 잘라낼 수 있다는 점을 보여주었습니다.

일단 weight pruning의 특징으로는, 어떤 weight이 어떻게 잘려나갈지 모르므로 unstructured pruning이자 automatic pruning의 한 종류로 분류될 수 있습니다. 하지만 이렇기 때문에 결과로 얻어진 희박한 구조를 실제 속도/용량 이득으로 가져오려면 하드웨어적인 특별한 처리가 필요하다는 단점이 있습니다. 그럼에도 불구하고 weight pruning이 계속 제기되는 이유 중 하나로는, 일반적으로 structured pruning에 비해 굉장히 많은 양의 weight들을 제거할 수 있기 때문입니다. 이는 아래 표를 보시면, 위의 다른 structured pruning과는 달리 95%라는 굉장히 많은 수치의 weight까지도 pruning을 시도했다는 사실을 보실 수 있습니다.

Weight Pruning에게 따로 section이 할당된 것을 보면, unstructured pruning의 경우 앞서 살펴보았던 structured pruning 기법들과 다른 무언가가 있음을 짐작할 수 있습니다. 가장 먼저 CIFAR 데이터셋들에 대한 결과를 보겠습니다. 80% 이하의 weight들을 pruning 한 경우, scratch-E는 가끔씩 fine-tune보다 좋지 못하지만 scratch-B의 경우 더 좋은 결과를 보여줄 수 있는 것처럼 보입니다. 하지만 95% 이상으로 굉장히 많은 weight들이 pruning 된 경우, fine-tuning은 from scratch 방법보다 좋은 모습을 보여주는 모습을 보여주고 있습니다. ImageNet과 같은 큰 benchmark에서는 이 모습이 더 두드러집니다. Scratch-E는 물론이고, 대부분의 경우에서 Scratch-B가 fine-tune보다 좋지 못한 모습을 보여주고 있습니다.
저자들은 이 현상이 굉장히 sparse한 network를 직접 학습시키는 것이 어렵다(CIFAR)라는 이유, 혹은 dataset 자체가 굉장히 학습시키기 어렵고 복잡하기 때문(ImageNet)에 unstructured pruning에서 scratch-B가 fine-tune보다 좋지 못한 모습을 보여준다고 가설을 세우고 있습니다. 또한 추가적인 제안으로, unstructured pruning은 structured pruning과 달리 가중치 분포를 기존과 굉장히 다르게 바꿔놓는다는 현상을 보이는데, 이것이 원인이 되지 않겠느냐는 주장을 하고 있습니다.

아쉽게도 저자들은 다른 unstructured pruning (<Dynamic Network Surgery, Guo et al., 2016>)으로 실험해 보지 않고 더 이상의 분석도 진행하지 않은 것처럼 보여 정확한 원인은 파악할 수 없지만, 그래도 굉장히 흥미로운 현상을 제시하여 해당 원인에 대해 추가적인 연구의 가능성을 던져주고 있습니다.
Network Pruning as Architecture Search
여기까지 우리들은 총 6가지의 기존 pruning 방법들에 rethinking 방법론을 실험하고, 그 결과 structured pruning의 경우 automatic이든 predefined이든 상관없이 scratch-B로 학습시키는 것이 일반적으로 좋은 성능을 보여준다는 점을 배울 수 있었습니다. 즉 기존의 pruning 방법론들에서 주로 찾고자 하는 것은 어떤 위치에 있는 특정 weight의 값이 중요하다는 것보다는, pruning 결과로서 남은 architecture 자체가 중요하다는 점을 시사하고 있습니다.
이 Section에서 저자들은, pruning으로 얻어진 모델들과 uniform하게 prune하여 얻어진 모델을 비교하여 automatic network pruning에서 행해지는 architecture 찾기의 가치를 보여주고 있습니다. 물론 이전에도 automatic network pruning과 architecture search의 관계점을 보여주고 있는 논문들은 많았지만, 이 논문에서는 weight 자체의 값은 아예 배제하고 architecture search 관점에서만 관계점을 보여주고 있다는 차이가 있습니다.
Parameter Efficient of Pruned Architectures

위의 그래프 중 왼쪽의 그래프는 Automatic Pruning 중 하나인 Network Slimming의 Pruning 결과와, 해당 Pruning 결과와 동일한 파라미터 수를 가지도록 모든 channel에서 uniform하게 prune을 진행한 결과를 비교한 모습입니다. 모든 경우에서 network slimming으로 얻은 architecture가 월등한 모습을 보임을 알 수 있어, 확실히 automatic pruning에서 얻어지는 architecture가 굉장히 efficient하다는 점을 알 수 있습니다. 오른쪽 그래프는 unstructured pruning인 magnitude based pruning으로 같은 실험을 진행한 결과며, 마찬가지로 uniform하게 prune 시켜서 얻은 구조보다 pruning을 거쳐 얻은 구조가 훨씬 efficient하다는 사실을 알 수 있습니다.
More Analysis
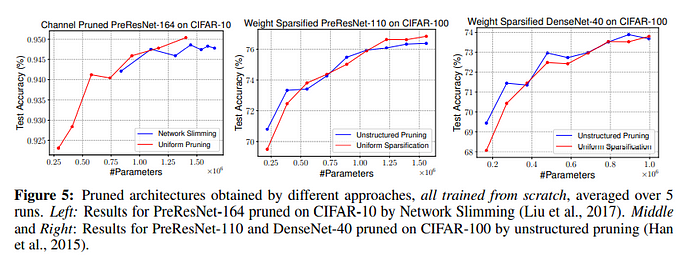
하지만 Uniform Pruning이 Automatic Pruning보다 항상 좋은 모습을 보여주지는 못했습니다. 위의 그래프에서 볼 수 있듯이, PreResNet이나 Desnet 같은 비교적 최신의 Network Architecture들에서는 automatic pruning과 uniform pruning 결과의 차이가 그리 크지 않다는 사실을 볼 수 있었습니다. 저자들이 해당 pruning 후 남은 weight의 비율을 stage 별로 살펴본 결과, 해당 구조들에서는 automatic pruning을 진행하더라도 stage 별로 거의 uniform하게 pruning을 진행하는 모습을 보였고, 따라서 uniform pruning과 거의 차이가 없게 되었다는 것을 알 수 있었습니다. 이는 VGG에서 automatic pruning 결과가 stage 별로 굉장히 non-uniform 하다는 점으로 뒷받침됩니다.
Generalizable Design Principles from Prune Architectures
저자들은 pruning에서 얻은 발견들을 바탕으로, architecture design 시 general하게 적용할 수 있는 원리들을 제안하고 있습니다. 이를 위해 저자들은 몇 가지 실험들을 진행했습니다.
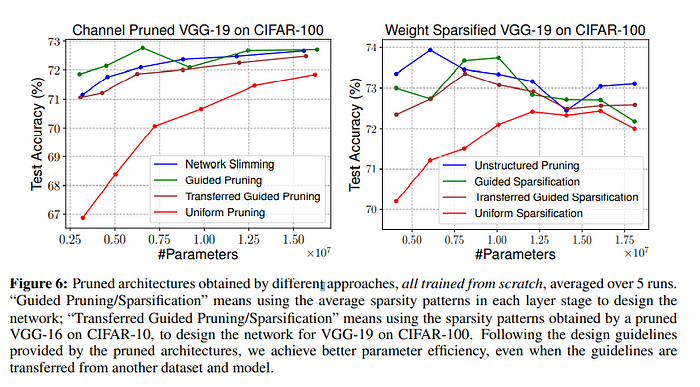
Network Slimming을 이용하여 pruning을 진행한 후의 architecture 결과에서, 각각 stage의 평균적인 channel 개수를 구하여 새로운 네트워크의 stage 별 channel 개수로 선정하였고 이를 ‘Guided Pruning’이라고 설정하였습니다. 마찬가지로 magnitude based pruning으로 얻은 average sparse pattern을 바탕으로 architecture kernel의 구조를 설계한 것을 ‘Guided Sparsification’이라 하였고, 그 결과는 unstructured pruning과 비슷한 성능을 보여줬습니다.
하지만 여기까지만 보면 그렇게 효율적인가에 대해서는 논란의 여지가 있을 수 있습니다. 따라서 저자들은, 해당 Guided design pattern을 pruning 대상이 되었던 architecture가 아닌, 별개의 architecture에 적용한 후 얼마나 효과적으로 해당 구조가 동작하는지 실험해보았습니다. 즉, VGG-16+CIFAR-10에서 얻은 Guided Architecture가 VGG-19+CIFAR-100에 적용되었을 때의 결과를 본 것입니다. 이는 논문에서 “Transferred Guided Pruning/Sparsification”이라 부르고 있습니다.
결과를 보면, Guided Pruning과 Transferred Guided Pruning 모두 좋은 결과를 내어, Guided를 이용하는 방법이 굉장히 효과적이라는 사실을 확인할 수 있었습니다.
Discussions with Conventional Architecture Search Methods
저자는 기존의 NAS, 즉 Neural Architecture Search 방법들과 위에서 설명한 Guided Pruning 방법을 짧게 짚고 넘어갑니다. 기존의 방법들은 보통 강화학습(reinforcement learning)이나, evolutionary algorithm (진화 알고리즘) 등을 사용하며, 굉장히 많은 반복을 통해 최적의 구조를 찾는 과정을 수행합니다. 반면에 Pruning을 응용하는 방법은 한 번의 pruning을 통해 구조를 찾을 수 있다는 간편함이 돋보이지만, 단점으로는 pruning을 통해서라면 기존 네트워크의 내재된, 즉 sub-network들로만 search space가 한정되는 문제가 있는 단점이 있습니다.
Experiments on the Lottery Ticket Hypothesis (Frankle & Carbin, 2019)
<Lottery Ticket Hypothesis>는 <Rethinking the value of network pruning>과 동일한 학회 (ICLR 2019)에서 best paper으로 선정된 논문으로, pruning 과정의 가중치 초기화에 대해 다루고 있다는 점에서 비슷한 점이 많습니다.
<Lottery Ticket Hypothesis> 논문에서는, 제목에 나타나 있듯이 한 가지 가설을 제시하고 있습니다. 큰 네트워크의 sub-network 중에서는 기존 네트워크와 비교했을 때 같거나 더 성능이 좋은 sub-network, 즉 winning ticket이 존재하는데, 이는 large network의 initialization과 관련이 있다는 점입니다. 이는 magnitude based weight pruning을 진행한 후, 해당 weight들을 fine-tune하거나 random re-initialization하는 것이 아니라, 원래 large network의 initialization 시 사용되었던 값을 가져왔을 때 competitive한 성능을 내는 실험으로부터 도출된 가설입니다. Rethinking 방법론과 비교해보면, Rethinking 논문은 원래 pruned model의 initialization 값과 trained 값보다는, 새로 random initialization을 이용한다는 점에서 차이가 보이지만, 결국 initialization에 대해 다루고 있는 것은 동일합니다.
따라서 얼핏 보면 이 둘은 서로 상반된 주장을 하고 있는 것처럼 보입니다. 하지만 세부적인 내용에서 몇 가지 차이가 있습니다. 가장 큰 차이로는, rethinking 논문은 structured pruning 방법들로 실험을 진행했지만, lottery ticket은 unstructured pruning에 대한 가설입니다. 또한 rethinking 논문에서는 큰 네트워크들에서 pruning 실험을 진행했지만, lottery ticket에서는 대부분이 6층 이하의 얕은 네트워크에서 실험이 진행되었습니다. 추가적으로 rethinking에서는 큰 learning rate의 momentum SGD optimizer를 사용하였지만 lottery ticket에서는 작은 learning rate의 Adam optimizer을 사용하였습니다. 마지막으로 rethinking에서는 ImageNet을 포함하였지만, lottery-ticket에서는 MNIST와 CIFAR만을 사용하였습니다.


저자들은 비교 실험으로, learning rate 차이로 인한 lottery-ticket과 rethinking 실험을 unstructured pruning에 적용하여 진행하였습니다. 결과를 정리해보면, winning ticket 실험은 learning rate 0.01로 진행할 때만 효과가 있었다는 모습을 보였습니다.
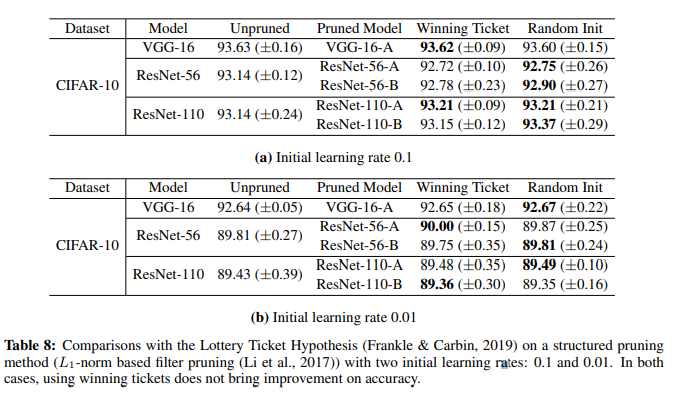
또한 Structured Pruning에 각각의 방법론을 적용한 결과, 큰 learning rate과 작은 learning rate 모두에서 lottery ticket 방법론과 rethinking 방법론의 결과가 거의 비슷한 것을 볼 수 있었으며, 다만 initial learning rate이 클 때 모델 자체의 정확도는 전반적으로 높은 것을 볼 수 있었습니다.
위의 결과를 바탕으로 저자들은 다음과 같이 정리합니다. 일단 winning ticket은 unstructured pruning, 작은 learning rate 상황에서만 정확도 향상 효과를 냅니다. 다만 이 작은 learning rate 상황이라는 것이 애초에 큰 learning rate의 경우보다 낮은 정확도를 가집니다. Lottery Ticket 논문에서 winning ticket의 효과가 ResNet-18, VGG를 큰 learning rate에서 학습시켰을 때 나타나지 않는 현상과 위의 실험을 바탕으로 생각해보면, winning ticket 방법론이 learning rate이 작을 때 효과적인 까닭은 최종 학습된 모델의 가중치가 작은 learning rate 때문에 처음 가중치 값에서 크게 달라지지 않기 때문일 것이라고 추측하고 있습니다.
논문 리뷰를 마무리하며
지금까지 지난 1편과 이번 2편을 통해 <Rethinking the value of network pruning>의 기본적인 내용과, 이를 토대로 기존 pruning 방법론들에 대한 전반적인 것들을 살펴보았습니다. 물론 여기에 소개된 방법들 이외에도, 굉장히 많은 방법으로 네트워크 모델을 최적화하고, 굉장히 많은 방법으로 가중치의 중요도를 산정하는 방법들이 지금도 제시되고 있습니다.
다만, 실제 응용 시에 pruning을 진행할 때에는, 이 논문에서 소개된 방법들로도 만족할만한 성능을 보여줄 것이므로, 혹시 관심있으신 분들은 이 논문의 저자가 정리한 Github Code를 응용하셔서 실험해 보시는 것도 추천드립니다.
또한 이 글을 통해, 지금까지는 그저 별 생각없이 잘 되는 네트워크 구조를 고르고 학습해보았다면, 더 효율적인 네트워크 구조란 무엇일까라고 한 번 생각해보실 수 있는 계기가 될 수 있으면 좋을 것 같습니다. 특히나 Pruning을 처음 접해보시는 분들이 이 글을 읽으셨다면, 앞으로 pruning에 대해 접하게 되셨을 때 “아 그거…!” 하고 알아보신다면 기쁘겠네요 :)
긴 글 읽어주셔서 감사합니다! 앞으로 다른 주제로 찾아뵙게 되더라도 관심 가져주세요! 물론 그 중에는 새로운 pruning method 등으로도 찾아뵙겠습니다.